2. Основные структуры

2.3. Функции и способы их задания

2.2 Операции с множествами 2.4 Числовые последовательности

Определение. Числовой функцией $f(x)$ мы будем называть отображение некоторого подмножества $A$ вещественной оси на некоторое подмножество $B$ вещественной оси. $A$ при этом называется областью определения, $B$ - областью значений функции $f(x)$.

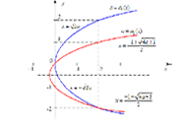
Функция может быть задана явной формулой, таблицей, графическим образом или словесным описанием.

Обратная функция. Если отображение $f(x)$ взаимно-однозначно, то можно каждому элементу $y \in B$ поставить в соответствие тот элемент $x \in A$, который переводится в $y$ отображением $f(x)$. Построенное отображение называется обратной функцией, она обозначается $x=f^{-1}(y)$. Таким образом, согласно определению, $x=f^{-1}(f(x))$, $y=f(f^{-1}(y))$.

Сложная функция. Пусть заданы числовые функции $y=f(x): A \rightarrow B$, $z=g(y): B \rightarrow C$. Тогда можно рассмотреть отображение $A \rightarrow C$, которое вычисляется следующим образом: $z=g(f(x))$. Эта числовая функция называется суперпозицией функций $f(x)$ и $g(y)$ или сложной функцией. Иногда такая функция обозначается $z=(g\circ f)(x)$.

Элементарные функции. Приведем список элементарных функций. Предполагается знакомство с ними в рамках школьного курса математики, так что читателю известны их области определения и области значений.

1. Степенная функция $y=x^{\gamma }. $

2. Показательная функция $y=a^x$.

3. Логарифмическая функция $y=log_a(x)$.

4. Тригонометрические функции $y=\sin x$, $y=\cos x$, $y=tg x$, $y=ctg x$, $y=\arcsin x$, $y=\arccos x$, $y=arctg x$, $y=arcctg x$.

5. Многочлены (полиномы). Функции вида \[ y=P(x)=a_0+a_1x+a_2x^2+...+a_nx^n. \] Числа $a_0,a_1,a_2,...,a_n$ называются коэффициентами многочлена. В многочлене присутствуют только целые неотрицательные степени переменной $x$, причем имеется конечное число слагаемых.

6. Дробно-рациональные функции. Функции вида \[ y=R(x)=\frac{P(x)}{Q(x)}, \] где $P(x),Q(x)$ - многочлены переменной $x$.

Задачи

2.2 Операции с множествами 2.4 Числовые последовательности

1. Введение

+2. Основные структуры

3. Пределы. Непрерывные функции +

4. Производная, дифференциальное исчисление+

5. Высшие производные+

6. Приложения дифференциального исчисления+

7. Первообразная (неопределенный интеграл)+

8. Техника вычисления первообразных+

9. Определенный интеграл+

10. Несобственные интегралы+

11. Интегралы зависящие от параметра+

12. Приложения определенных интегралов+

2. Основные структуры

2.3. Функции и способы их задания